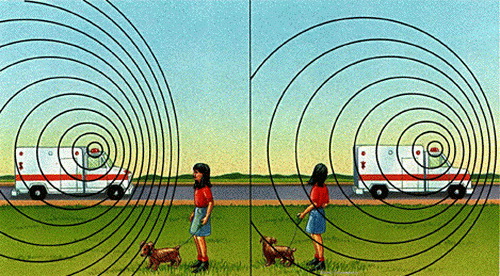
Относительное изменение длины волны
Эффе́кт До́плера — изменение частоты и, соответственно, длины волны излучения, которая воспринимаетсянаблюдателем, вследствие движения источника излучения и/или движения наблюдателя.
Мотоциклетные гонки привлекают всегда десятки тысяч зрителей из ближних и дальних мест. Плотной толпой окружают они асфальтированную дорогу, жадно вдыхая воздух, насыщенный запахом бензина и… сенсацией. Далекий шум моторов звучит музыкой для их ушей. А затем мимо зрителей в одиночку и группами проносятся сверкающие машины. На них, наклонившись вперед, сидят причудливые фигуры водителей. Мотоциклы видишь только считанные секунды, когда они проносятся мимо с такой скоростью, что едва успеваешь различить большие номера на них. Соперничество гонщиков и одновременно борьба человека с машиной — всё это опьяняет толпу.
Хотя там присутствуют десятки тысяч зрителей, которые ясно слышат звук работающих моторов, найдётся только несколько сотен человек, которые обратят внимание на одну особенность. И вряд ли отыщется хотя бы один, который задумается о том, что в этом оглушительном реве моторов можно обнаружить своеобразнейшее физическое явление.
Машины приближаются к нам, издавая пронзительный звук, но в момент, когда они проносятся мимо, высокий тон внезапно переходит в низкий. Этот скачок по высоте тона составляет терцию или даже кварту. Мотор, равномерно поющий при своём неистовом вращении, имеет два голоса. С высоким звуком он несётся на нас, с низким — уносится вдаль
Если бы покойный пражский профессор математики Христиан Допплер (1803-1853) мог присутствовать при гонках, он определённо получил бы от этого огромную радость. Возможно, во время одного из перерывов, он, полный воодушевления, забрался бы на одну из стоящих кругом лестниц-стремянок и обратился к ошеломленным зрителям со следующей речью:
«Глубокоуважаемые дамы и господа! Шум, идущий от этих новомодных машин, есть не что иное, как частая последовательность уплотнений воздуха, образующихся в результате периодического выброса продуктов сгорания интенсивно работающими моторами. Число таких колебаний, происходящих в 1 сек, настолько велико, что мы слышим звук. Итак, закройте глаза и соблаговолите как следует прислушаться! Этот звук имеет определённую частоту f соответственно числу оборотов двигателя. Колебания распространяются в воздухе и проходят в 1 сек определённое расстояние с, соответствующее скорости звука. Упомянутые уплотнения бегут в воздухе одно за другим, поэтому на отрезке с располагается f колебаний. Расстояние от одного уплотнения до следующего называется длиной волны. Из всего сказанного следует, что
длина волны λ = c : f
Если эта огненная машина приближается к вам, глубокоуважаемые зрители, со скоростью v, то вы должны разместить f колебаний на более коротком отрезке с — v, так как скорость звука с не может изменяться.
Тем самым звуковые волны становятся короче, и в ваши драгоценнейшие уши попадает больше колебаний, чем в том случае, когда машина стоит. Вместо звука с частотой f вы слышите более высокий звук. Пожалуйста, будьте добры, ещё раз обратите на это внимание. То, что вы при этом слышите, ценнее, чем вся входная плата!
Итак, каждая волна становится короче на величину Δλ. Общее укорочение всех f волн составляет тогда f х Δλ и равно отрезку v, на который сокращается весь проходимый звуковыми волнами путь. Это даёт нам уравнение f х Δλ = v. Теперь будьте любезны разделить обе его части на f. Если вы вспомните, что f = с : λ , то получите Δλ = (v х λ) : с и отсюда
относительное изменение длины волны Δλ : λ = v : c
Если машины удаляются от нас, всё получается аналогично, только теперь волны соответственно растягиваются и величина Δλ в последнем уравнении означает в этом случае соответствующее увеличение длины волны. Как вы сами изволите совершенно отчётливо заметить, получается низкий звук. Подробнее вы можете прочитать об этом в моем сочинении «О цветном свете двойных звёзд», вышедшем в Праге в 1842 г.»
Сам Допплер так и не узнал, какие замечательные последствия имело его открытие. Оно создало абсолютно новые возможности определения «лучевой» скорости небесных тел, т. е. скорости, с которой они удаляются или приближаются к Земле.
Уравнение Δλ : λ = v : c годится также и для светового излучения, которое, подобно звуку, представляет собой волновое явление. Нахождение скорости v сводится к измерению величины Δλ — изменения длины волны определённой линии спектра. Какого эффекта можно достичь этим способом, полностью зависит от того, в состоянии ли применяемый спектроскоп измерить эту весьма малую величину.
Разрешающая способность хорошего призменного спектрографа достигает λ : Δλ = 50000. С дифракционной решёткой, для развития и совершенствования которой так много сделал Фраунгофер, можно достичь значения 200000, а в интерференционных спектрографах — даже 4000000.
Эффект Допплера на краях вращающегося Солнца
В качестве примера возьмём вращение Солнца, о существовании которого можно заключить по движению солнечных пятен. Очень мощная линия Фраунгофера Н, которая принадлежит кальцию, имеет длину волны λ = 396,8475 нм (нм — сокращённое обозначение нанометра, т. е. одной стомиллионной части метра). Измерения на одном крае солнечного диска дают λ несколько больше, а именно, 396,8500 нм, а на противоположном, наоборот, только 396,8450 нм (рис. 60). Поэтому Δλ = 0,0025 нм. Отсюда по уравнению Δλ : λ = v : c получаем линейную скорость вращения на поверхности Солнца = 1890 м/сек. Простой расчёт даст нам период вращения 26,8 суток.
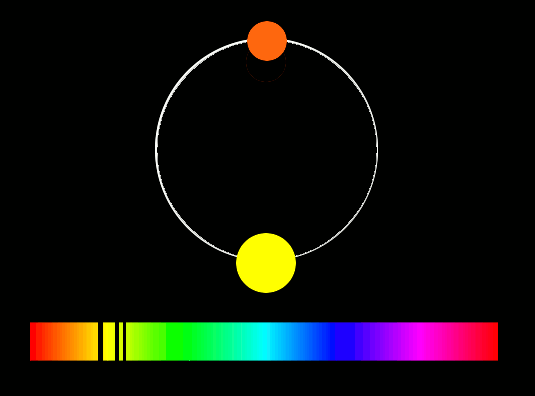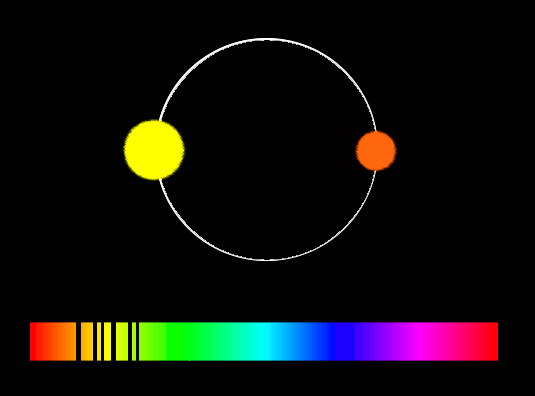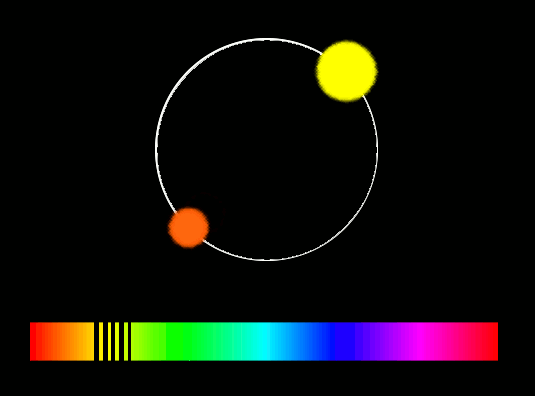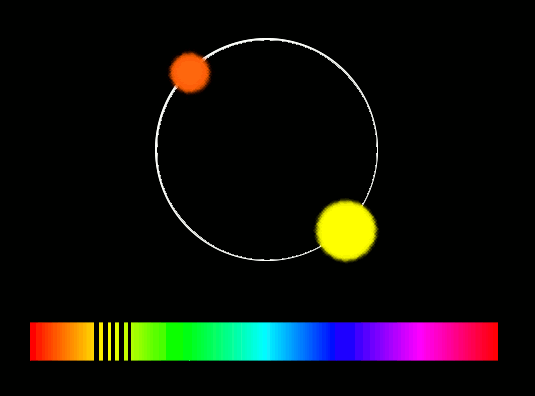
Таким же методом определяют орбитальные скорости двойных звёзд. Если смотреть на плоскость их орбиты с ребра, то одна из звёзд приближается к наблюдателю, в то время как другая удаляется. Сдвиг линий, одинаковый для обеих звезд, имеет максимальное значение тогда, когда их расхождение максимально.
Очень часто расстояние между членами системы настолько мало, что в телескоп они видны, как одна звезда. В этом случае получают также и единый спектр. Оба сдвига линии Δλ, которые должны происходить в противоположных направлениях, в этом спектре проявляются одновременно, спектральные линии периодически удваиваются, и по этому признаку можно обнаружить, что речь идёт о двух звёздах, которые обращаются вокруг общего центра масс.
Такие системы, которые могут быть обнаружены только благодаря эффекту Допплера, уловимому при помощи спектрографа, носят название спектрально-двойных звезд.