Световой год
Мы с детства слепо убеждены в том, что луч света — это идеально прямая линия. Все измерения длин и углов без света были бы немыслимо трудны. Не только потому, что в темноте ничего не видно, но и по той причине, что не существует другого физического объекта, о котором можно со спокойной совестью утверждать, что он безупречно прямой.
Так как линейка и рулетка слишком коротки для измерения космического пространства, приходится в этом случае полностью положиться на свет. При этом космические расстояния измеряют точно так же, как это делает на поле землемер. Берут определённый базис, длина которого заранее известна, и из его конечных точек визируют объект (светило). Угол, заключённый между двумя визирными линиями, даёт возможность рассчитать расстояние до него. Этот угол называют параллаксом. С таким же успехом можно начать измерения с самого объекта и сказать:
параллакс светила — это угол, заключённый между двумя прямыми, направленными от светила в два различных наблюдательных пункта.
Рис. Суточный параллакс
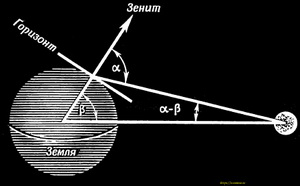
Колоссальные космические расстояния требуют также и базиса соответствующей величины. Для измерений в пределах солнечной системы в качестве базиса используют радиус Земли (рис.). Когда светило в течение суточного оборота Земли достигает своей наивысшей точки, луч, направленный на него, и перпендикуляр к земной поверхности, проходящий через точку наблюдения, образуют угол α. Если теперь соединить прямой это светило с центром Земли, то получим угол β. Разность между двумя углами α — β называется суточным параллаксом светила.
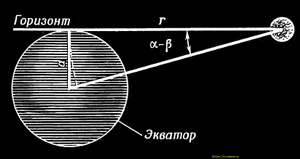
Рис. Экваториальный горизонтальный параллакс
Угол α достигает своего максимально возможного значения, а именно 90°, когда светило расположено на горизонте. Если наблюдатель находится одновременно и на экваторе, то получают особый случай экваториального горизонтального параллакса (рис.). Хотя треугольник, построенный на радиусе Земли, как на основании, является в этом случае прямоугольным, из-за малости угла α — β можно использовать известное соотношение:
Угол в радианной мере = Длина дуги/Расстояние.
Равенство справедливо, так как дуга окружности (изображения пунктиром на рис.) практически совпадает с радиусом Земли. Отсюда находим
Расстояние R = Радиус Земли α/Параллакс.
Например, параллакс Луны равен а = 0°,95068. Этот угол составляет в радианной мере α = 0,01659 и расстояние Земля — Луна R = 6378 км/0,01659 = 384400 км.
Для измерения расстояния до звезд радиус Земли слишком мал. Здесь надо перейти к значительно большему базису; в этих случаях используют половину диаметра земной орбиты. Многие звёзды, расположенные сравнительно близко к Земле, в течение года описывают на небосводе большие или меньшие эллипсы. Однако это только кажущееся смещение; оно является следствием изменения нашего местоположения. Если измерить большую полуось такого эллипса в угловых единицах, то получим годичный параллакс звезды (рис.).
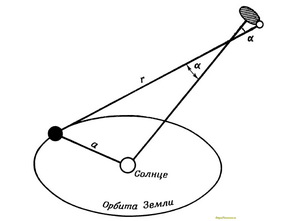
Рис. Годичный параллакс
Хотя в сравнении с рассматриваемыми гигантскими расстояниями базис, равный половине диаметра земной орбиты, довольно мал, всё же он ещё достаточен для многих звезд, находящихся в относительной близости к нам. Ближе всего к Земле находится звезда Проксима в созвездии Центавра — очень слабая звезда, которая в наших северных широтах не видна. Её параллакс составляет 0″,765. Используя этот же самый способ, который мы только что применили для Луны, и зная радиус орбиты Земли 149,6 х на 10 в 6 степени км, получаем расстояние до Проксимы Центавра 4,034 х на 10 в 13-й степени км.
Наше воображение настолько несовершенно, что мы не можем представить себе такие огромные числа. Чтобы сделать их более удобными для сравнения и вычислений, ввели две особые единицы измерения. Одна из них — параллакс-секунда, сокращенно парсек, пс. Это расстояние до объекта, годичный параллакс которого составляет одну угловую секунду. Расстояние до Проксимы Центавра равно — 1,31 пс. Отсюда также легко можно найти
1 nc = 3,0857 х 10 в 13-й степени км.
Другая, тоже довольно часто применяемая единица, световой год, возможно, немного нагляднее. Световой год — это путь, который свет проходит за один год, точнее в течение времени 31,557 х 10 в 13-й степени сек. Так как скорость света с = 299 790 км/сек, то расстояние в один световой год равно произведению этих двух чисел, а именно:
1 св. год. = 9,4605 х 10 в 12-й степени км;
1 пс = 3,26 св. года..
Легко сказать: один световой год. Но попробуйте себе представить соответствующее ему расстояние! Это невозможно, и все сравнения только приводят нашу мысль на край новой пропасти. Можно попытаться преодолеть это расстояние на ракете, летящей со второй космической скоростью. Но перед стартом следует предупредить пассажиров такой ракеты, что их путешествие будет продолжаться 27 000 лет!

Можно сравнить это расстояние с расстоянием от Земли до Солнца; тогда обнаружим, что один световой год длиннее радиуса нашей орбиты более чем в 6 млн. раз. Ни один портной не рискнёт представить себе нить толщиной с человеческий волос и длиной в один световой год, так как масса такой нитки должна составлять 200 млн. тонн! Впрочем, все более или менее искусственные попытки представить световой год при помощи привычных понятий ничего не изменяют ни в его размерах, ни в том факте, что наиболее близкая звезда Проксима Центавра удалена от нас на расстояние 4,26 св. года. По сравнению с другими звёздами и звездными системами это расстояние ещё можно назвать очень небольшим.
Однако, поскольку точность измерений при помощи тригометрических методов ограничена величиной +-0″,03, пользуясь этими методами, мы не можем проникнуть сколь угодно далеко. В самом лучшем случае можно определить расстояние порядка 100 св. лет.
Для измерения ещё больших расстояний приходится прибегать к совершенно другим методам. Там имеют дело уже с миллионами световых лет. От наиболее удалённых небесных тел нас отделяет не меньше 3 млрд. св. лет. Точнее надо сказать так: три миллиарда лет они находились на том месте, откуда сегодня до нас дошёл свет. Как обстоит дело с ними в настоящее время, мы узнаем только ещё через три миллиарда лет. Тому, кто очень спешит это узнать, придётся подождать.