
Нормальное увеличение телескопа
Если пучок параллельных лучей света проходит мимо непрозрачного края экрана, то на противоположной стене должна появиться тень. Приглядевшись внимательнее, мы увидим, что тень не имеет резкой границы, а немного размыта. В этом случае луч света отклоняется от своего прямолинейного направления, или, как говорят, дифрагирует.
Р и с. 1. Дифракция света в случае простой щели
Если свет проходит через щель между двумя такими экранами (рис. 1), то все отдельные лучи светового пучка претерпевают одно и то же отклонение. Для простоты мы принимаем, что речь идёт о пучке параллельных лучей.
По большей части после прохождения через щель они распространяются дальше также прямолинейно. На стене появляется светлое изображение щели — так называемый главный максимум или максимум 0-го порядка.
Из многих отклоняющихся в сторону лучей мы рассмотрим два. Один из них (1) лежит в верхней, другой (1′) в нижней половине пучка, и оба должны отклониться от прямой линии на одинаковый угол α. Этот угол выберем так, чтобы нижний луч 1′ как бы отставал от верхнего луча 1 точно на половину длины волны. Тогда окажется, что в одном из лучей гребень, а в другом впадина волны всегда бегут рядом. Эти лучи накладываются друг на друга (интерферируют), и в данном случае их взаимодействие приводит к тому, что они гасят друг друга. То же самое происходит для всех других подобных пар лучей, которые распространяются от отверстия под тем же самым углом. Поэтому на соответствующем месте экрана получается тёмная полоса. Это так называемый первый минимум.
Теперь рассмотрим больший угол отклонения, который выберем так, чтобы взаимное смещение лучей 2 и 2′ составляло как раз целую длину волны. Тогда интерференция приведёт к взаимному усилению, так как теперь два гребня или соответственно две впадины волны в этих лучах всякий раз совпадают. На экране снова будет светлая полоса, правда, не такая светлая, как главный максимум, так как интенсивность лучей света с увеличением угла отклонения все более падает. Это — максимум 1-го порядка и т. д.
В результате получим следующую картину: по обе стороны от главного максимума возникает система тёмных и светлых интерференционных полос. При ширине щели d мы можем записать формулу, характеризующую положение первого минимума при дифракции от простой щели
sin α = λ/d
Эту формулу несложно вывести из геометрических соотношений, данных на рис. 55. Аналогичная картина получается, если отверстие круглое, как в пустой гильзе от зрительной трубы. Тогда возникает система концентрических интерференционных колец, которую не может устранить даже самая лучшая линза (рис.2).
Р и с.2. Различимость изображений двух точек Р1 и Р2
В интересах наглядности на рис. 1 и 2 действительные соотношения линейных размеров и углов сильно искажены. Чтобы интерференционные полосы (или кольца) возникали на достаточной площади, используемая щель (или круговая диафрагма) должны иметь очень малые размеры. Расчёт приводит нас к следующей формуле:
Угловое расстояние первого минимума после прохождения луча через круглое отверстие
α = 140″/d
где d — диаметр отверстия в миллиметрах.
Итак, если свет приходит от двух различных точек, то на экране вместо изображения двух точек возникают две системы тёмных и светлых колец. Если точки лежат очень близко друг к другу, то эти кольцевые системы перекроют друг друга и превратятся в одну. Чтобы можно было различить изображения, они должны быть сдвинуты одно относительно другого настолько, чтобы вместо одного светлого пятна в главном максимуме образовалось два отдельных пятна. Минимальный сдвиг, при котором получается такая картина, будет тогда, когда первый минимум одной кольцевой системы попадёт примерно на середину главного максимума другой, так как в этом случае образуются два светлых пятна, разделённых тёмной зоной.
Поэтому формула α = 140″/d даёт в то же время минимальный угол, который должен быть заключён между лучами, исходящими из двух точек, чтобы эти точки можно было видеть раздельно. Чем больше диаметр отверстия d, через которое свет попадает в оптический прибор, тем ближе друг к другу могут лежать рассматриваемые точки. В этом и заключается сущность рассматриваемой проблемы:
Разрешающая способность оптического прибора тем выше, чем больше диаметр его отверстия.
В настоящее время диаметр отверстия более 1 м имеют только зеркальные телескопы. Большой современный телескоп обсерватории Маунт Паломар (Калифорния, США) имеет зеркало диаметром 5,1 м и с фокусным расстоянием 16,8 м. Его разрешающая способность а = 140″/5100 = 0″,028.
Нетрудно рассчитать, что этот телескоп позволяет различить на Луне две точки, наименьшее линейное расстояние а между которыми составляет 52 м. Линейное расстояние между двумя точками при данном угле α, согласно зависимости, равно α = r х α; в данном случае r — расстояние до Луны, равное 384400 км, и α = 0″,028; отсюда по расчёту наименьшее линейное расстояние а между которыми и составляет 52 м.
Человеческий глаз, как оптический прибор, тоже имеет ограниченную разрешающую способность. Её можно оценить величиной α = 120″ или иногда 140″. Задача телескопа состоит в том, чтобы увеличить угол, определяемый формулой α = 140″/d, до данного значения угла α.
Отсюда следует, что так называемое полезное увеличение телескопа:
v = d,
где d — диаметр объектива (мм).
Полезное увеличение телескопа на Маунт Паломар с диаметром зеркала d = 5,1 м составляет, следовательно, v = 5100. Получаемые посредством этого телескопа изображения можно увеличить до любого формата. Но от этого число деталей в них не прибавится, снимки будут только выглядеть всё более крупными и размытыми.
Невелика польза от дальнейшего увеличения растянутых объектов, составленных из многих видимых точек (как, скажем, поверхность планет, Луны или Солнца). Применяя соответствующий окуляр, можно делать изображение сколь угодно большим. Но число различимых точек на каждой единице поверхности от этого больше не становится. Выигрывая в размерах, мы теряем в резкости изображения, и все дополнительные расходы практически затрачиваются впустую.
Когда рассматривают точечные объекты, как, например, звёзды, выявляется другая сторона проблемы. Из-за своего ничтожного видимого диаметра звезды даже после самого сильного увеличения остаются только точками, которые предстают в виде дифракционных колец. В этом случае телескоп выполняет уже другую задачу. Он должен собрать возможно большее количество доходящего до нас света, а также сделать видимыми звёзды, не различимые невооруженным глазом. Свет, собранный объективом, попадает через окуляр в зрачок нашего глаза.
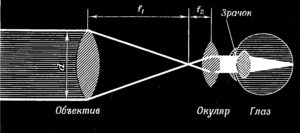
Р и с. 3. Нормальное увеличение: пучок лучей света, попадающий в объектив диаметра d, суживается до диаметра зрачка
На рис. 3 изображён поток параллельных лучей света, идущий от одной звезды. Он падает на объектив диаметром d. Телескоп собирает эти лучи и направляет их в зрачок глаза. Чтобы все лучи могли попасть в глаз, диаметр сконцентрированного пучка не должен быть больше диаметра зрачка. Ночью последний составляет около 8 мм. Из рис. 3 можно заключить, что диаметр объектива и зрачка должны находиться в том же отношении, что и фокусные расстояния f1 к f2. Но это отношение, равно увеличению v телескопа. Отсюда имеем формулу
v = Диаметр объектива : Диаметр зрачка.
Если подставить сюда диаметр зрачка 8 мм, то получим нормальное увеличение телескопа
v = d : 8,
где d — диаметр объектива в миллиметрах.
Это выглядит так, как если бы сильное увеличение и здесь не имело смысла; в самом деле, количество света, попадающее в глаз, не станет больше, если световой пучок, созданный окуляром, сделается ещё тоньше. Однако здесь для нас важно то обстоятельство, что чем больше увеличение, тем темнее становится фон неба, а кроме того, появляются звёзды, которые прежде нельзя было заметить.
При фотографировании неба условия проще, так как светочувствительная пластинка располагается непосредственно в фокальной плоскости объектива. Тогда, при прочих равных условиях, сила света зависит только от диаметра объектива. Так как свет падает на принимающую поверхность, сила света растёт пропорционально квадрату диаметра объектива.
Кроме того, разрешающая сила телескопа сильно зависит от различных побочных обстоятельств, таких, как потери света в его оптической системе, неизбежные искажения получаемых изображений, помутнение атмосферы и колебания слоев воздуха, через которые проходят лучи от светил.
Насколько неспокойствие земной атмосферы мешает наблюдениям, видно хотя бы из того, что Паломарский телескоп теоретически (для острого глаза с α < 60″) может давать увеличение в 20000 раз, но из-за влияния атмосферы увеличение больше чем в 3000 раз использовать не удаётся.

