Закон Стефана — Больцмана
Во Вселенной разбросано бесчисленное множество солнц, подобных нашему. Светимость одних намного больше светимости Солнца, других — намного меньше. Из всех них лишь одно находится достаточно близко, чтобы мы могли воспользоваться его теплом. Остальные — по крайней мере с нашей точки зрения — расточают свою энергию в окружающее пространство, абсолютно не заботясь о том, приносит она кому-нибудь пользу или нет.
Однако в нашем мире существуют ещё меньшие по размерам солнца, которые тем не менее очень полезны. Они изготовляются на фабрике, и их можно по недорогой цене купить в любом универмаге. А дома достаточно вставить штепсель в розетку и миниатюрное солнышко приятно согреет замерзшие ноги или опухшую щеку. Такая электрическая лампа-грелка хотя и не так горяча, как её старший родственник — Солнце, но имеет с ним кое-что общее, а именно мощность её излучения удовлетворяет одному и тому же закону.
Закон Стефана — Больцмана:
Мощность излучения Р = δ х АТ4
Если подставить постоянную δ = 5,67 х 10-8 вт/м2 х град4, площадь поверхности А излучаемого тела в м2 и абсолютную температуру Т в градусах Кельвина, то получим мощность излучения в ваттах (рис. 1).
Рис. 1. Закон Стефана — Больцмана: при увеличении абсолютной температуры вдвое мощность излучения абсолютно черного тела повышается в 24 = 16 раз
Этот закон и особенно постоянная δ соответствуют только абсолютно чёрному телу. Такое тело имеет свойство поглощать все лучи, падающие на его поверхность. В холодном состоянии оно кажется очень чёрным, как сажа или как мышиная нора.
По сравнению со всеми остальными телами оно также и излучает максимальное количество энергии.
Закон Стефана — Больцмана говорит о суммарном количестве энергии излучения, но умалчивает о том, из чего это излучение состоит. А оно представляет собой непрерывный спектр электромагнитных волн. Если при помощи чувствительного приёмника излучения исследовать отдельные участки длин волн, то можно определить, что энергия излучения имеет характерное распределение на различных участках.
Рис. 2. Кривые излучения абсолютно чёрного тела
Получается кривая (рис. 2) с ярко выраженным максимумом, соответствующим определенной длине волны. Чем выше температура излучающего тела, тем выше и острее будет максимум кривой. Площадь под этой кривой становится все больше, так как излучаемая мощность быстро растёт с повышением температуры.
Если сделать временное допущение, что звёзды подчиняются этому закону, то можно легко рассчитать их температуру, когда известна площадь их поверхности А и мощность излучения Р. Мощность излучения Солнца определена, она равна Р = 3,85 х 1026 вт.
Его диаметр составляет d = 1,392 х 109 м. Тогда формула Р = δ х АТ4 даёт нам так называемую эффективную температуру Солнца 5785° К.
Так как пользование законом Стефана — Больцмана предусматривает знание площади поверхности звезды и тем самым ее радиуса r, то этот способ применим только для немногих близких звёзд, для которых мы можем определить требуемые величины.
Кроме того, не надо забывать ещё и о том, что этот закон полностью применим только к абсолютно чёрному телу и, следовательно, не вполне точен для звёзд. Тем не менее эффективная температура — важная характеристика звёзды. Для многих звёзд она лежит между 3000 и 50000° К.
Абсолютная величина звёзды М, как и мощность излучения, должна зависеть от её температуры и диаметра. По закону Стефана — Больцмана получается, что
абсолютная болометрическая величина звёзды — М = 4,62 — 10 lg Т — 5lg d.
Здесь температура Солнца Тс = 1 и диаметр Солнца dс = 1.
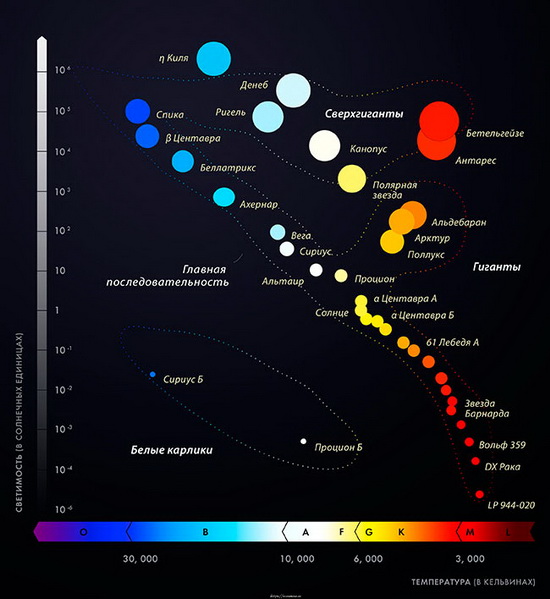
Чтобы проверить, какой результат нам даёт это соотношение, вернёмся ещё раз к спутнику Сириуса. Так как мы уже оценили общую массу системы Сириуса в 3,35 и массу главной звёзды в 2,35 масс Солнца, масса спутника получается равной 3,35 — 2,35 = 1 массе Солнца.
Вызывает удивление тот факт, что этот всё же очень массивный спутник Сириуса имеет видимую величину только + 8m,6 и едва различим в телескоп. Поэтому он должен иметь очень малые размеры. Чтобы рассчитать его диаметр, нам надо знать только его абсолютную величину. Она оказывается равной М = + 11,4. Если принять далее температуру Сириуса В равной температуре Солнца, то член 10 х lg Т в равенстве будет равен 0, так как Т = 1 и lg l = 0. Для диаметра d получаем lg d = (4,62 — 11,4) : 5 = 0,64 — 2 и d = 0.044 диаметра Солнца.
Отсюда легко найти плотность Сириуса В. Плотность Солнца равна. 1,41 г/см3, и для Сириуса В мы получаем 16500 г/см3. Это в 2000 раз больше плотности железа!
Поэтому Сириус В представляет собой исключительно интересный объект для изучения. Это так называемый белый карлик. Замечательно, что существуют и такие белые карлики, плотность которых составляет несколько сотен килограммов на 1 кубический сантиметр.
