Конечна или бесконечна Вселенная?
Чтобы нагляднее представить себе расширение Вселенной, прибегнем снова к аналогии. Наш трёхмерный мир представим в виде поверхности шара. Если мир не точно сферический, это в принципе ничего не меняет.
Возьмём резиновый баллон и подставим его на одно мгновение под ливень капель краски, создаваемый малярным ручным распылителем. На круглой поверхности баллона лягут тогда все «звёздные системы» этого мира. Они будут распределены здесь произвольно, но в общем и целом равномерно в виде маленьких пятнышек краски. Каждое из этих пятнышек представит «галактику», насчитывающую примерно 200 млрд, звезд.
Выберем произвольно одну такую точку Р1 (рис. 1). Пусть это наша система Млечного Пути. Вторая точка Р2 удалена от неё на расстояние а, третья — Р3 — на удвоенное расстояние 2а.
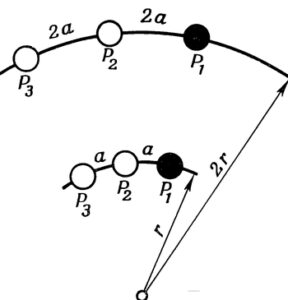
Рис. 1. Скорость разбегания туманностей как следствие расширения Вселенной.
Теперь начнём надувать баллон. Мир будет расширяться, и точки станут отдаляться друг от друга. Если за время t радиус r баллона удвоится, то удвоится и расстояние между всеми точками. Точка Р2 будет удалена теперь от Р1 на расстояние 2а, Р3 от Р1 — на расстояние 4а.
Тогда скорости по отношению к точке P1 составят
для точки: Р2: v2 = (2a — a) : t = a : t;
для точки: Р3: v3 = (4a — 2a) : t = 2a : t.
Мы видим, что это точно соответствует закону, характеризующему разбегание туманностей: скорости пропорциональны расстояниям от центра наблюдения. Но это пригодно не только для исходной точки P1, но и для любой точки нашей забрызганной краской поверхности. Ни одна точка не может посягнуть на какое-то особенное положение.
Таким образом, наше пространство не имеет центра, все точки шаровой поверхности равноправны. Разбегание туманностей выглядит одинаково независимо от того, из какой звездной системы мы смотрим.
Поразмыслив, мы могли бы ещё сослаться на внутренность баллона, которая у нашей модели должна быть полой. Но она вовсе не полая! Каждая точка поверхности баллона была внутри его до того, как она начала всё более и более удаляться от его центра. Благодаря этому такая модель мира имеет замечательное свойство: она даёт достаточно места для всего прошлого и будущего.
Теперь вернёмся к нашему реальному миру.
Если бы расширение происходило непрерывно и равномерно, то радиус r сферической Вселенной, показанный на рис. 1, по мере нашего возвращения в прошлое должен был бы становиться всё меньше и меньше.
Постоянная Хаббла имеет значение 0,25 х 10-17 сек-1 или, что то же самое, 75 км/сек-Мпс. Это означает, что точка, которая в данный момент находится от нас на расстоянии в 1 Мпс = 3,09 х 1019 км, секунду назад находилась на 75 км ближе. Время, которое должно было пройти, чтобы точка достигла такого удаления, легко рассчитать:
Т = (3,09 х 1013 км) : 75 км/сек) = 4,11 х 1017 сек, или 15 млрд. лет
Этот расчёт вытекает из предпосылки, что когда-то давно вся Вселенная была сжата до одной единственной точки. Всё вещество Вселенной, вся огромная его масса вместе с принадлежащей ей энергией миллиардов известных сегодня небесных тел была сконцентрирована в одной точке или по меньшей мере в очень маленьком пространстве.
По неясным причинам потом произошёл колоссальный взрыв, после которого материя начала разлетаться в пространстве в разные стороны и с этого момента вступила на нынешний путь своего развития.
С этим расчётом согласуется единственное обстоятельство, которое является, правда, довольно волнующим. Дело в том, что интервал времени 15 млрд. лет соответствует приблизительной оценке возраста Земли.
При этом исходили из того, что радиоактивный уран, пройдя многочисленный ряд распадов, превращается в устойчивый свинец. Исследуя процентное содержание урана и свинца в различных минералах, можно довольно легко рассчитать время, за которое образовалось имеющееся количество свинца.
Отсюда получается, что около 5 млрд. лет назад существовало естественное равновесие в составе химических элементов. Если ввести поправку на время, за которое элементы образовались из первичной плазмы, и, может быть, немного исправить постоянную Хаббла, то это совпадение в самом деле поразительно.
Мы рассказали об этой модели мира потому, что именно она чрезвычайно много описывалась и обсуждалась. Однако ещё совсем не доказано, действительно ли Вселенная замкнута в себе описанным образом.
Так же хорошо можно себе представить, что расширение происходит в обычном трёхмерном пространстве. Все галактики сохраняют в соответствии со своей инерцией ту скорость, которую они получили в начале своего «разбегания».
Тогда галактики с самыми большими скоростями также должны быть наиболее удалёнными от нас, если мы прежде всего примем, что точка их старта лежала вблизи нашей собственной Галактики.
Все галактики в целом образуют тогда сферическое пространство. Так как они могут иметь скорость, самое большее равную скорости света с, то произведение всего прошедшего времени Т на эту скорость даёт нам современный радиус мира R = = сТ. Подставив значение Т, которое мы рассчитали ранее, получим R = 3 х 105 км/сек х 4,11 х 1017 сек = 12,3 х 1022 км = 13 млрд. св. лет.
Итак, эта модель мира повсеместно открытая. Она бесконечна, в то время как модель, которую мы рассмотрели перед этим, конечна и замкнута в себе. Применяя специальную теорию относительности, можно также привести доказательства того, что в этой открытой модели мира любую точку Вселенной можно рассматривать как начальную. Распределение материи в пространстве однородно, как и в первом случае.
Но, по-видимому, вопрос о том, конечна или бесконечна наблюдаемая нами Вселенная, нельзя решать безоговорочно. Надо прежде всего учитывать многие астрофизические данные и включать их в рассмотрение этого вопроса. Именно таким образом получаются модели мира, замкнутого и бесконечного в одно и то же время.