Основные постулаты общей теории относительности
Специальная теория относительности, хотя она и явилась одним из гениальнейших творений человеческого разума, которое только мог создать один человек, ещё не удовлетворила самого Эйнштейна.
Прежде всего сказывалось то обстоятельство, что лежащее в её основе преобразование Лоренца было выведено только для системы отсчёта, движущейся равномерно, а не ускоренно. К этому несовершенству теории присоединилась ещё и нерешённая проблема тяготения.
Хотя ньютоновский закон тяготения был известен уже довольно давно и на его основе удалось построить общую небесную механику, обладающую точностью, которая до сегодняшнего дня едва ли оставляет желать чего-либо лучшего, природа тяготения по-прежнему не была выяснена.
Поэтому Эйнштейн в течение многих лет стремился к тому, чтобы расширить своё творение и довести его до общей теории относительности. Это должно было способствовать решению обоих основных вопросов.
Но что, однако, представляет собой ускоренная система отсчёта? Если мы сидим в вагоне, который полностью изолирован от внешней среды, а поезд идёт идеально равномерно и без всяких толчков, то никакие средства не помогут нам установить, движется ли вообще наш вагон. Совсем другое дело, если поезд начнет ускорять своё движение или внезапно резко затормозит. Тут портфели и чемоданы выскочат из багажных сеток, а люди, стоящие в коридоре, начнут спотыкаться и падать друг на друга (рис. 1).
Рис. 1. Ускоренная система отсчёта
Всё ограничится извинениями и вежливым смехом, так как ни один человек не в состоянии что-либо сделать против этой внезапно возникшей силы инерции. Ведь это было не что иное, как инерция, которая дремлет в каждом теле и сразу превращается в силу, если система отсчёта изменяет своё равномерное движение. До тех пор пока сохраняется ускорение, продолжает действовать и сила инерции.
Во вращающейся кабине действуют такие силы, которые отсутствуют в равномерно и прямолинейно движущемся поезде. Это центробежная сила, которая отбрасывает все предметы в сторону от оси вращения. Это также сила инерции, которая возникает потому, что массе «навязан» характер движения, который ей противоречит согласно первой аксиоме Ньютона.
Таким образом, различие между равномерно и ускоренно движущимися системами отсчёта очевидно. В первой удовлетворяются законы Ньютона, например закон инерции, а во второй — нет. В то время как равномерно и прямолинейно движущиеся системы невозможно отличить друг от друга, ускоренная система тотчас выдаёт себя наличием и величиной сил инерции, которые в ней действуют.
Кроме инерции, масса обнаруживает ещё свойства тяжести. Прежде всего можно легко доказать, что сила тяжести является только частным случаем силы инерции. Для этой цели сядем в лифт какого-нибудь достаточно высокого здания. В тот момент, когда наш спутник уже собрался зажечь свою сигару, вдруг рвётся канат, и лифт устремляется вниз (рис. 2).

Рис. 2. Исчезновение силы тяжести при свободном падении
Хотя задуманный эксперимент и кажется немного жестоким, однако шахта на случай падения лифта снабжена специально встроенными хитроумными приспособлениями, так что ничего страшного случиться не может. Кроме того, предположим, что здание достаточно высокое, чтобы у нас хватило времени для проведения различных наблюдений.
Они будут очень интересными. Сначала человек останется стоять с раскрытым ртом, но сигара не упадёт вниз. Она повиснет в воздухе перед его испуганным лицом и терпеливо будет «ждать» спичку.
Это произойдет потому, что человек и сигара падают вниз с одинаковым ускорением. Сам человек не будет чувствовать больше своего веса — сила тяжести внезапно исчезнет. Даже спичка «не захочет» больше гореть. Она будет только коротко вспыхивать, чтобы тотчас снова погаснуть, ибо горячие продукты сгорания не поднимаются вверх.
Мы констатируем
Первое: для внешнего наблюдателя сила тяжести существует как до начала, так и во время падения; для наблюдателя внутри она исчезла.
Иными словами, в лифте господствует точно такое состояние, как в пространстве, лишённом силы тяготения, — где-нибудь в космосе, вдалеке от всех притягивающих небесных тел.
Если бы лифт находился в таком месте, где действительно отсутствует сила тяжести, то можно было бы продолжить эксперимент. Представим себе, что какой-то мощный подъёмный кран вдруг захватывает канат и тянет лифт вверх с постоянным ускорением а = 9,81 м/сек2 (рис. 3).
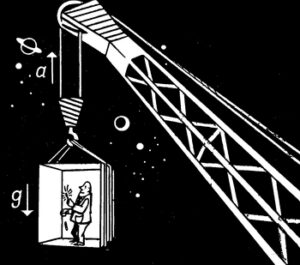
Эффект поразительный! Человек снова чувствует свой вес и твёрдый пол под ногами. Спичка опять как ни в чем не бывало загорается. Но теперь для курения нужна сигара, которая тем временем упала на пол. В кабине установились полностью земные условия, как если бы она прочно и спокойно стояла на земле и, несмотря на это, как мы узнали ещё в поезде, всё это только проявление силы инерции. Она заменяет теперь поле тяготения, которого совсем не существует. Но нет! Сила тяготения здесь подлинная, и мы констатируем
Второе: для наблюдателя, находящегося снаружи, сила тяжести исчезла, а для наблюдателя внутри она существует.
Тем самым мы создали ситуацию, из которой исходил Эйнштейн при создании общей теории относительности. То, что инертная и тяжелая массы пропорциональны друг другу, это отнюдь не случайность и не обман — они даже идентичны. Сила тяжести возникает и исчезает, если переходить от одной системы отсчёта к другой, которая движется ускоренно по отношению к ней.
Отсюда видно, что общая теория относительности ставит перед собой задачу установить ту закономерность в природе, которая не зависит от выбора системы отсчёта. Движение тела тогда протекает таким образом, что для описания его в неподвижной системе отсчета нужны силы, которые исчезают или, наоборот, появляются в другой системе, движущейся относительно этой системы ускоренно.
Поэтому проблемы, поставленные перед общей теорией относительности, намного труднее, чем вопросы специальной теории. Там ставится только одна задача — правильно преобразовать длину, время и массу.
Здесь же надо при смене систем отсчета вводить новые силы и притом такие, которые точно соответствуют действительности. Необходимый для этой цели математический аппарат очень сложен.
В результате получена система уравнений, которые описывают состояние поля тяготения в пространстве и времени. Они похожи на уравнения Максвелла, описывающие электромагнитное поле. Эти уравнения позволяют совершать преобразования физических законов в любой системе отсчёта, причем сила тяготения естественно фигурирует здесь среди других сил.