
Виды траекторий полёта
Знания скорости на старте далеко не достаточно, чтобы попасть на одно из многочисленных небесных тел. Правда, при хорошей погоде цель видна довольно хорошо, она не качается и спокойно позволяет взять себя на мушку. Но что только не случается за длительный промежуток времени, пока снаряд находится в полёте!
Небесное тело, на которое необходимо попасть, движется по сложной кривой вокруг Солнца, причём одновременно меняется его удаление от Земли. При этом перемещается также связанное с ним поле тяготения. Оно оказывает влияние на снаряд задолго до того, как он попадает в цель. Но это ещё не всё.
Так как прямое падение на исследуемое небесное тело приведёт к неминуемому разрушению летательного аппарата, нужно стремиться произвести «мягкую посадку». Для этого необходимо заранее располагать надёжными сведениями о свойствах поверхности этого небесного тела, изучив его с достаточно близкого расстояния.
Такие данные можно получить, если облететь это тело по близкой орбите и вернуться обратно. Уже доказано, что такая задача практически разрешима. 4 октября 1959 г. третья советская космическая ракета, несущая автоматическую межпланетную станцию «Луна-3», облетела Луну по заранее рассчитанной петлеобразной траектории и в течение 40 мин станция делала снимки обратной стороны Луны.
Решение всех связанных с этой проблемой частных вопросов мы можем предоставить специалистам в области астронавтики. Но нам остаётся ответить на основной вопрос: как в общем случае движется снаряд, находящийся в поле тяготения, будь то поле тяготения Земли или небесного тела, к которому он летит?
До сих пор мы рассматривали только круговую траекторию или вылет в поле тяготения по прямолинейному пути. А как ведёт себя тело, летящее в поле тяготения с произвольно направленной скоростью? Такая задача полностью и математически точно решена ещё Ньютоном 300 лет назад.
Рассматривая эту задачу, мы снова будем исходить из допущения, что масса сосредоточена в одной точке. Действительные размеры небесных тел не оказывают на движение никакого влияния, так как все эти тела приблизительно шарообразны. Их размеры проявляются только в том, что в определённых случаях снаряд проходит теоретическую траекторию не до конца: траектория прерывается, когда снаряд достигает поверхности небесного тела, или при старте траектория начинается не из центра тела, а с его поверхности.
В таком случае геометрический вид траектории определяется только двумя величинами: кинетической энергией W-кин и потенциальной энергией W—пот в каждой определённой точке траектории. При этом безразлично, удаляется ли тело от притягивающего центра или приближается к нему. Закон, определяющий траекторию, в одинаковой степени верен как при старте, так и во время приближения к цели.
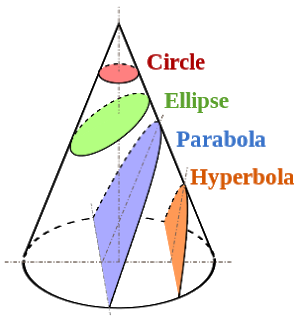
Возможны следующие три вида траекторий:
парабола: W-кин = W—пот,
гипербола: W-кин > W—пот,
эллипс: W-кин < W—пот
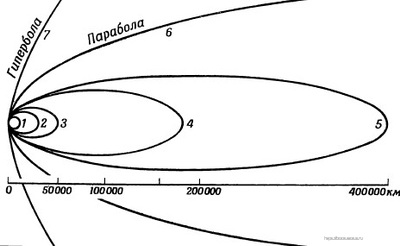
Рис. Орбиты искусственных спутников Земли.
Начальные скорости:
Круговая орбита (I) — 7,9 км/сек
Эллипс (2) — 10,0 км/сек
Эллипс (5) — 10,5 км/сек
Эллипс (4) — 11,0 км/сек
Эллипс (5) — 11,1 км/сек
Парабола (6) — 11.2 км/сек
Гипербола (7) — 16,7 км/сек
Все три кривые принадлежат к так называемым «коническим сечениям» .
1. Параболическая траектория
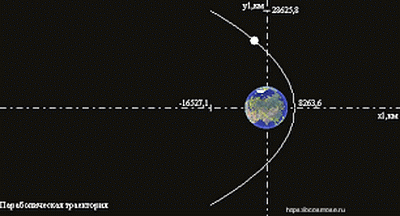
Парабола — кривая, разомкнутая с одной стороны, причем обе её ветви в бесконечности идут параллельно друг другу. Центр поля тяготения лежит в фокусе параболы. Для осуществления полёта по параболической траектории необходимо, чтобы кинетическая энергия летящего тела была в каждый момент точно равна потенциальной энергии, которую имеет это тело по отношению к притягивающему центру.
Нужна так называемая «критическая скорость», необходимая для вылета из поля тяготения соответствующего небесного тела. Итак, если летящее тело приближается к Земле с любого направления и имеет в какой-нибудь точке своего пути скорость, равную критической скорости, соответствующей расстоянию в этот момент до Земли, то это тело обогнёт центр Земли по параболической траектории и после этого снова уйдет в бесконечность. Ради простоты мы не учитываем при этом влияния поля тяготения Солнца.
Однако такое возвращение в бесконечность может не состояться, если параболическая траектория пересечёт где-нибудь поверхность Земли. Тогда летящее по более или менее наклонной кривой тело в этом месте столкнётся с земной поверхностью, имея в момент столкновения скорость 11,2 км/сек.
Правда, после этого удара тело может снова стартовать с той же скоростью 11,2 км/сек. Новая траектория будет также ветвью параболы. Поэтому вторую космическую скорость называют иногда параболической скоростью.
Возможен горизонтальный старт — по параболической траектории, касательной к земной поверхности, причем точка касания совпадает с вершиной этой параболы. Если же старт происходит вертикально, тело преодолеет поле тяготения в радиальном направлении. Парабола превратится в прямую линию, и обе её ветви совпадут.
2. Гиперболическая траектория
Гипербола состоит из двух отдельных симметричных ветвей, имеющих свой фокус. Небесную механику интересует только одна из этих ветвей — именно та, в фокусе которой лежит центр поля тяготения. В противоположность параболе обе ветви гиперболы в бесконечности идут не параллельно друг другу, а приближаются к двум прямым (асимптотам), которые образуют между собой определённый угол.
Тело летит по гиперболической траектории, если его скорость в любой точке пути больше параболической скорости, соответствующей этой точке. Приближение к небесному телу происходит так же, как и при параболической траектории. Разумеется, теоретически ничто не мешает стартовать с гиперболической скоростью.
3. Эллиптическая траектория
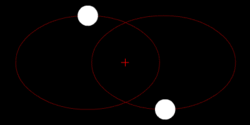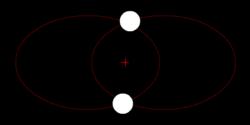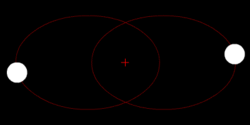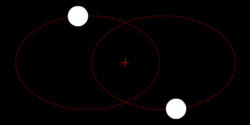
В соответствии с первым законом Кеплера, центр притяжения находится в одном из фокусов эллипса. Эллипс — замкнутая кривая. По такой траектории тело движется только в том случае, если его скорость меньше критической скорости в любой рассматриваемой точке траектории. Поэтому каждое тело, которое улетает с Земли со скоростью меньшей 11,2 км/сек, должно описывать эллипс. При этом безразлично, под каким углом это тело стартовало. Исключение составляет упомянутый выше вертикальный старт, когда эллипс становится бесконечно узким и превращается в прямую линию.
Окружность тоже можно рассматривать как эллипс. Мы знаем, что тело, улетевшее с земной поверхности в горизонтальном направлении со скоростью 7,9 км/сек, облетает Землю по круговой орбите. Если телу была сообщена та же скорость, но под каким-то углом к поверхности, то оно не может выйти на круговую орбиту, а движется по эллиптической, нисходящая ветвь которой пересекает земную поверхность. Точно так же ведёт себя тело, запущенное хотя и горизонтально, но со скоростью меньшей 7,9 км/сек. Оно также должно будет упасть на Землю.
Последний случай представляет не что иное, как обычный горизонтальный бросок. Могут сразу же возразить, что при этом должна получиться «баллистическая парабола», но противоречие улаживается благодаря практике. А именно в условиях движения вблизи поверхности Земли поле тяготения можно рассматривать как однородное и с практически достаточной точностью принимать, что ускорение силы тяжести постоянно на любой высоте.
Однако в действительности это не совсем так, поэтому все баллистические параболы в действительности являются эллиптическими кривыми, хотя их отклонение от параболической формы имеет только теоретическое значение.
Все эти соотношения приобретают, так сказать, обратный смысл, если летательный аппарат приближается к другому небесному телу. Если при этом скорость полёта меньше, чем соответствующая критическая скорость, летящее тело будет захвачено полем тяготения того космического объекта, к которому оно летит.
Пусть, например, снаряд захвачен Луной; это означает, что скорость его полета была меньше критической скорости на Луне, равной 2,4 км/сек. Поскольку это произошло, появляются две возможности: или этот снаряд превратится в спутник, который будет облетать Луну по эллиптической орбите, или эллиптическая орбита пересечет лунную поверхность и полет снаряда закончится.
Выйти на круговую орбиту вокруг Луны — такая задача требует от техники в её сегодняшнем состоянии подлинного искусства, ибо здесь необходимо точно согласовать между собой три величины: расстояние до Луны, соответствующую скорость полёта по круговой орбите и направление полёта точно по касательной.
